备注
Go to the end to download the full example code.
参数识别¶
这是一个参数识别的简单例子。压缩模型是一个 1x1x1 米立方体的简单模型。下表面固定,上表面承受 100 Pa 的压力。目标是找出能使最大位移达到 -0.1 米的材料的杨氏模量。
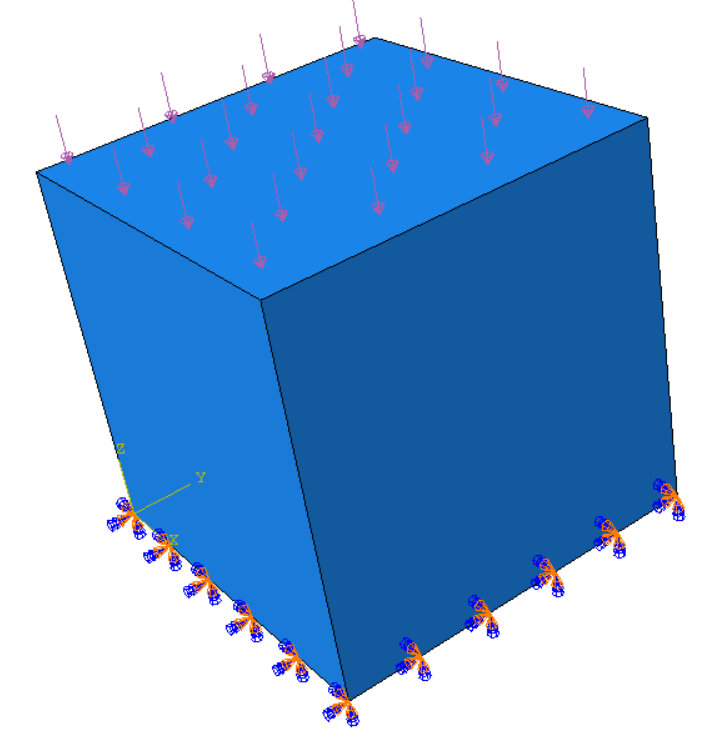
图 3 一个简单的压缩模型。¶
从理论上讲,材料的杨氏模量可以用下面的公式计算出来:
\[E = \frac{\sigma}{\epsilon} = \frac{P}{u_{\max}/h} = \frac{100}{0.1 / 1.0} = 1000\]
此脚本的输出为:
Search results:
modulus fitness
0 10.0 9.774944
1 100.0 0.887494
2 1000.0 0.001251
3 10000.0 0.090125
4 100000.0 0.099013
5 1000000.0 0.099901
Best modulus=1000.0 with fitness=0.0012505635619163569
The model script of this example can be found here.
import os
import numpy as np
import pandas as pd
def fitness(x: float, maxdisp_expected: float = -0.1):
# Change the working directory to a new folder
wd = os.path.join(os.path.dirname(__file__), f"Job-E={x}")
os.makedirs(wd, exist_ok=True)
os.chdir(wd)
# Run the model and read the output, the additional argument can be read by the Abaqus/Python script
os.system(f"python ../compression.py {x},0.2")
# Read the output and calculate the fitness
data = pd.read_csv("data.csv")
maxdisp = data["U3"].iloc[-1]
return abs(maxdisp - maxdisp_expected)
def grid_search(search_space: list[float], expected: float):
fs = []
for x in search_space:
print(f"Running model for E={x}")
fs.append(fitness(x, expected))
argmin = np.argmin(fs)
best = search_space[argmin]
print("Search results:", pd.DataFrame({"modulus": search_space, "fitness": fs}), sep="\n")
print(f"\nBest modulus={best} with fitness={fs[argmin]}")
return best
if __name__ == "__main__":
E = grid_search([1e1, 1e2, 1e3, 1e4, 1e5, 1e6], -0.1)
由 Sphinx-Gallery 生成